复习直方图与条形图

发表于 分类于 ， 阅读次数： 本文字数： 4.5k

0. 前言

在用python实现正态分布等概率分布函数时，混淆了直方图和条形图，又由于概率论没学到位，导致实现中遇到了不小的困难。

因而，借此篇博客复习一下，高中所学的直方图和条形图。。。

1. 直方图

1.1. 理解

首先，举一个直方图的例子：

2

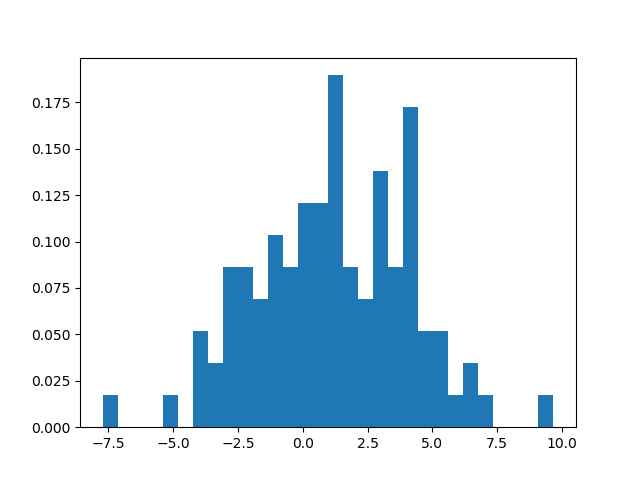
显然，直方图就是有很多根柱子的图。

假设，数据集合X是分布在实数集上的随机数集合，|X|=100。

对于直方图中的每个柱子：

  • 其宽对应横轴上的一个区间；

  • 其高对应集合X中属于该区间的数的个数。

频数分布直方图 (归一化直方图) 是直方图中的一种，它的特殊在于：

  • 其高对应该区间的计数除以集合X中的总数，即代表该区间的频数。

上述例子便是一张频数分布直方图。

1.2. python代码实现

1
2
3
4
5
6
7
8
9
10
11
import numpy as np
from matplotlib import pyplot as plt

x = np.random.normal(1,2,100) # 生成100个服从 N(1,2^2) 的正态分布的随机数

value, bins, count = plt.hist(x, bins=30, normed=True) # 根据x中的数据，画有30个连续区间的频数直方图
plt.show()

print('value:', value, len(value))
print('bins:', bins, len(bins))
print('count:', count)

输出：

3

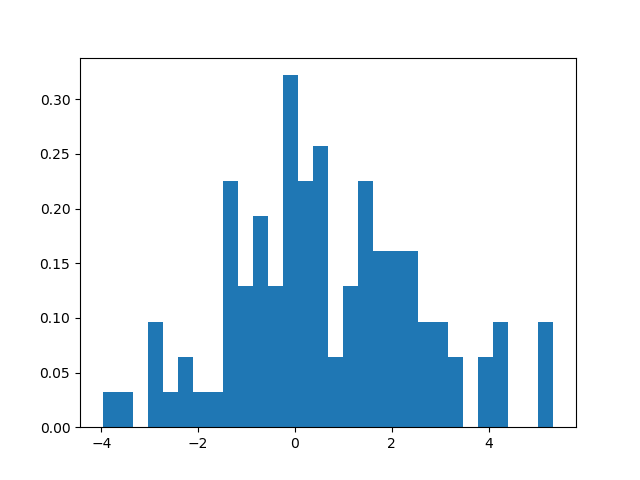
1
2
3
4
5
6
7
8
9
10
11
12
value: [0.03220688 0.03220688 0.         0.09662064 0.03220688 0.06441376
 0.03220688 0.03220688 0.22544816 0.12882752 0.19324128 0.12882752
 0.3220688  0.22544816 0.25765504 0.06441376 0.12882752 0.22544816
 0.1610344  0.1610344  0.1610344  0.09662064 0.09662064 0.06441376
 0.         0.06441376 0.09662064 0.         0.         0.09662064] 30
bins: [-3.97482069 -3.66432802 -3.35383536 -3.04334269 -2.73285002 -2.42235735
 -2.11186468 -1.80137201 -1.49087934 -1.18038668 -0.86989401 -0.55940134
 -0.24890867  0.061584    0.37207667  0.68256934  0.993062    1.30355467
  1.61404734  1.92454001  2.23503268  2.54552535  2.85601801  3.16651068
  3.47700335  3.78749602  4.09798869  4.40848136  4.71897403  5.02946669
  5.33995936] 31
count: <a list of 30 Patch objects>

对于plt.hist()函数：

  • params参数：

    • x: x轴上的数据集

    • bins: 表示划分区间的个数，即柱子的个数

    • normed: 表示是否归一化，若为True，则显示频数直方图

    • ……

  • return返回值：

    • value: 每个区间对应的y值

    • bins: 每个区间上下限的x值，如果有30个区间，则len(bins)为31

    • count: 区间的个数

其详情见官网

2. 条形图

2.1. 理解

举个栗子：

1

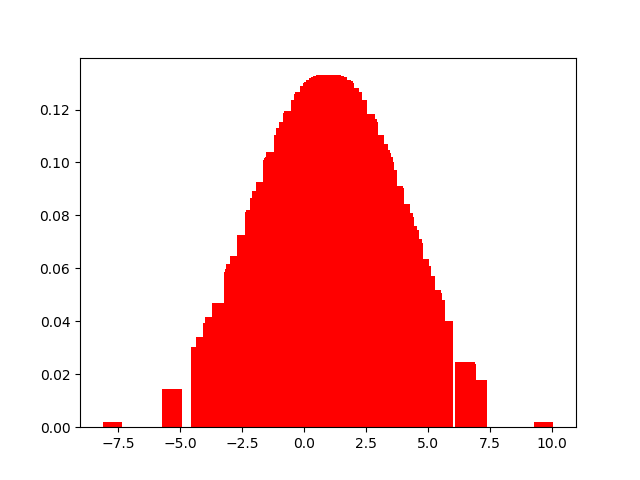
条形图似乎也是一个很多柱子的图。这便是条形图与直方图容易混淆的原因了。但，条形图的柱子似乎细很多呢。

其实，条形图相对直方图，更好理解。

条形图中，横坐标代表x值，纵坐标代表y=f(x)值。所以，条形图的边界就是对应函数f(x)图像的一部分了。

2.2. python代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import numpy as np
from matplotlib import pyplot as plt

'''正态分布公式'''
def normal_distribution(mean, standard, x):
    return (1 / (standard * np.sqrt(2*np.pi)) * np.exp(-(x-mean)**2 / (2 * standard**2)))

x = np.random.normal(1,2,100) # 生成100个服从 N(1,2^2) 的正态分布的随机数
print('x:', x)

y = normal_distribution(1,2,x)
print('y:', y)
plt.bar(x, y) # 画条形图。横轴为x，纵轴为y。
plt.show()

输出：

4

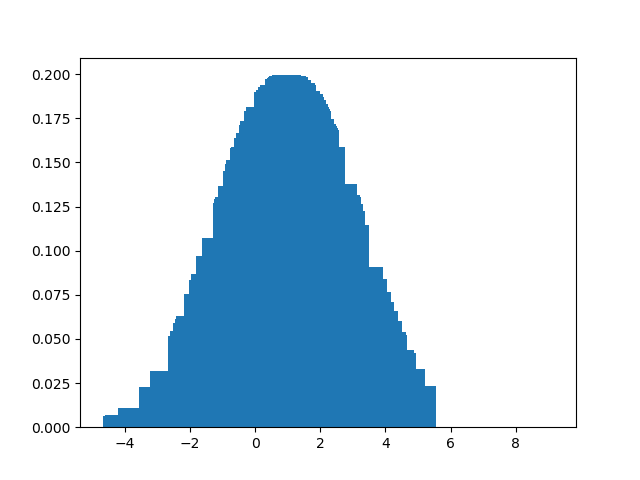
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
x: [ 1.76932332  0.36522094  5.1450445   0.05004145  1.7720948   2.72576013
 -0.10808016  1.89746125  3.63410412  2.91262325  4.10054093 -0.89758685
  1.11546737  4.27508464  0.76085493  1.47257128  4.5245259   2.34713613
 -0.05875876  8.75851437 -0.86486252 -0.34872341  0.07018679  0.88436324
  0.48392354  0.1297039  -0.59002276  3.10785551  1.3165206   2.71668659
  2.11486526 -0.84586926 -0.3576636   2.09204617  0.53542808  4.48640303
 -0.52501128 -2.04203587 -1.57609217  0.92228732 -2.28138689  1.92260707
  1.94208858  3.98329461 -4.28621987  0.0471915  -4.21319167  0.80202259
  3.875302    2.73255094 -1.40581636  1.17265753 -2.22711288  1.1008017
  1.87824436  3.10236217  1.43048658  1.00748939  4.80039664  0.8898163
  2.82500036  1.7141756  -1.2301184   1.16866276  1.66890047  0.6901983
  1.42811743  1.22482293 -0.25517217  1.78918545 -2.82314372 -1.79081425
 -0.48748191  2.9755605  -2.07325393  1.17953198  3.76772486  0.41385189
  0.83417547  1.15602977 -3.80374808 -1.63877772  2.14545695  3.10734999
 -3.17789913  1.86693313  0.41279216  2.02547252  1.60170928  1.83176309
  4.23187971 -0.3603266  -0.73596668  1.21855677 -2.12121712 -0.20157449
  0.06652799  2.84224194  2.15910299  3.5127497 ]
y: [1.85246481e-01 1.89672995e-01 2.32893302e-02 1.78192943e-01
 1.85147586e-01 1.37467642e-01 1.71089936e-01 1.80366335e-01
 8.37935889e-02 1.26267617e-01 5.99793484e-02 1.27175126e-01
 1.99138981e-01 5.21903254e-02 1.98050247e-01 1.93979816e-01
 4.22195850e-02 1.58987025e-01 1.73390851e-01 1.07673843e-04
 1.29147548e-01 1.58902008e-01 1.79038432e-01 1.99138006e-01
 1.92939699e-01 1.81452272e-01 1.45423186e-01 1.14467130e-01
 1.96988707e-01 1.38005420e-01 1.70767673e-01 1.30290347e-01
 1.58422143e-01 1.71846040e-01 1.94161674e-01 4.36539516e-02
 1.49151436e-01 6.27351432e-02 8.70200197e-02 1.99320615e-01
 5.19214540e-02 1.79337425e-01 1.78524921e-01 6.55729800e-02
 6.06572758e-03 1.78072195e-01 6.67586408e-03 1.98496245e-01
 7.09694403e-02 1.37064685e-01 9.67543721e-02 1.98729228e-01
 5.42654299e-02 1.99217948e-01 1.81137321e-01 1.14798536e-01
 1.94903532e-01 1.99469742e-01 3.27955468e-02 1.99168661e-01
 1.31543984e-01 1.87150614e-01 1.07124430e-01 1.98763102e-01
 1.88621259e-01 1.97092356e-01 1.94953096e-01 1.98214821e-01
 1.63814947e-01 1.84531071e-01 3.20922985e-02 7.53458647e-02
 1.51274227e-01 1.22463700e-01 6.12557886e-02 1.98669094e-01
 7.65643798e-02 1.91085957e-01 1.98786691e-01 1.98865040e-01
 1.11469968e-02 8.35358669e-02 1.69298023e-01 1.14497623e-01
 2.25067310e-02 1.81584831e-01 1.91056259e-01 1.74901040e-01
 1.90644952e-01 1.82945965e-01 5.40569843e-02 1.58278875e-01
 1.36861850e-01 1.98283670e-01 5.90225768e-02 1.66533569e-01
 1.78885926e-01 1.30508407e-01 1.68633817e-01 9.05978680e-02]