递归与非递归的转换（树的非递归遍历）

0. 前言

递归是计算机中基本而实用的算法思想。

主要用于解决有边界的重复性操作问题，即满足数学归纳法特性的问题。比如斐波那契数列。

可递归却有不少缺陷：运行效率低下、递归过多容易栈溢出等等。

但作为一把锋刃的解题利器，我们也不能抛弃它。众所周知，递归的本质即为栈，它运行在内存中，受操作系统控制，一个函数就是栈中的一个单位(栈帧)。递归的过程，就是内存中栈的入栈出栈操作。

因而，我们必然可以用自定义的栈来实现这个过程，即将递归转化为非递归。

那如何快速地将一个递归程序转化为一个非递归程序呢？我想用树的先、中、后序遍历的求解，来简单表述我的一己之见。

1. 树的先、中、后序遍历(递归模式)

1.1. 先中后序遍历解释

对于一棵树，先序遍历先输出根结点的数据、再输出左孩子树的数据、最后输出右孩子树的数据。简而言之，输出顺序为根—左—右。

以此类推，中序和后序遍历的输出顺序分别为：左—根—右、左—右—根。

1.2. 示例

对于如下的一棵树：

       A
   B       C
D     E      F
    G   H     J
  I    K  L

先序遍历：ABDEGIHKLCFJ
中序遍历：DBIGEKHLACFJ
后序遍历：DIGKLHEBJFCA

1.3. 递归实现遍历

先中后序遍历一棵树，代码十分简单。如下：

// 树的数据结构
typedef struct BTNode {
    char data;
    BTNode *lchild, *rchild;
}BTNode, *BiTree;

// 先序遍历，递归
void preOrderTraverse(BiTree bTree) {
    if (bTree) {
        cout<<bTree->data;               // 先输出根节点的数据
        preOrderTraverse(bTree->lchild); // 输出左子树的数据
        preOrderTraverse(bTree->rchild); // 输出右子树的数据
    }
}

// 中序遍历，递归
void inOrderTraverse(BiTree bTree) {
    if (bTree) {
        inOrderTraverse(bTree->lchild);
        cout<<bTree->data;
        inOrderTraverse(bTree->rchild);
    }
}

// 后序遍历，递归
void postOrderTraverse(BiTree bTree) {
    if (bTree) {
        postOrderTraverse(bTree->lchild);
        postOrderTraverse(bTree->rchild);
        cout<<bTree->data;
    }
}

2. 非递归遍历

2.1. 递归到非递归转换分析

对于递归的非递归转换，我们以函数栈的角度去解析就十分简单了。

以中序的递归遍历为例：

typedef struct BTNode {
    char data;
    BTNode *lchild, *rchild;
} BTNode, *BiTree;

// 中序遍历，递归
void inOrderTraverse(BiTree bTree) {
    if (bTree) {
        inOrderTraverse(bTree->lchild);
        cout<<bTree->data;
        inOrderTraverse(bTree->rchild);
    }
}

当主函数inOrderTraverse(bTree)中第一个inOrderTraverse(bTree->lchild)子函数被调用时，主函数中剩余的数据和步骤被保留在当前的函数栈帧中。而子函数入函数栈，成为栈顶函数。当子函数运行结束，返回时，子函数出栈，栈顶又变为主函数。然后，程序继续执行主函数中的剩余步骤。

同理子函数的子函数也是如此操作。过程如下：

主函数入栈：

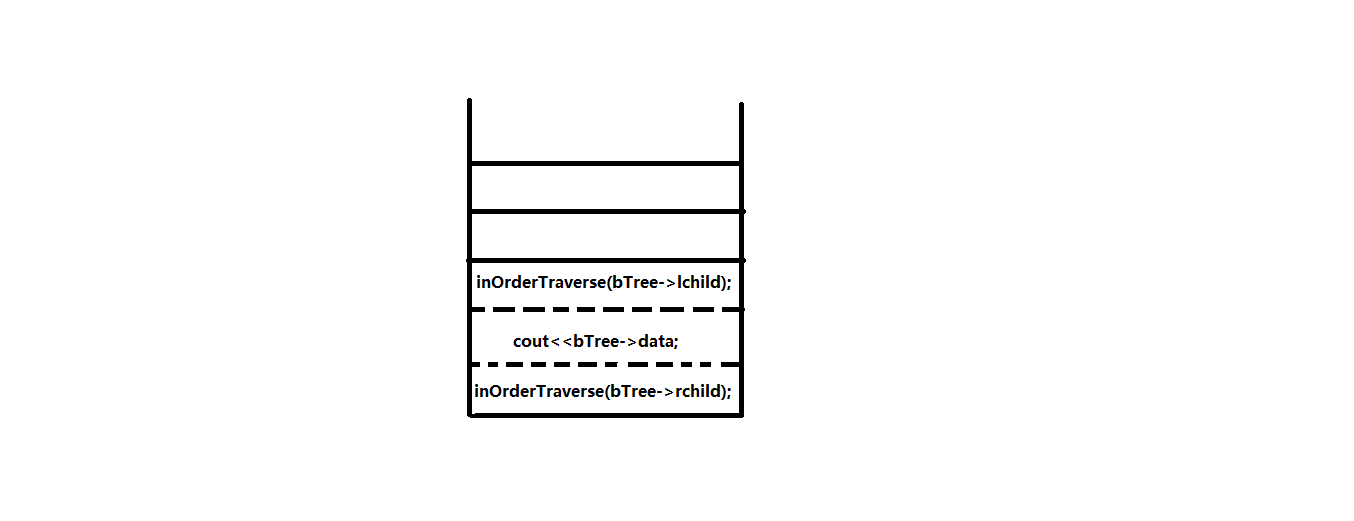
主函数调用第一个子函数的操作出栈，剩余步骤保存在栈中，而被调用子函数(蓝色)入栈：

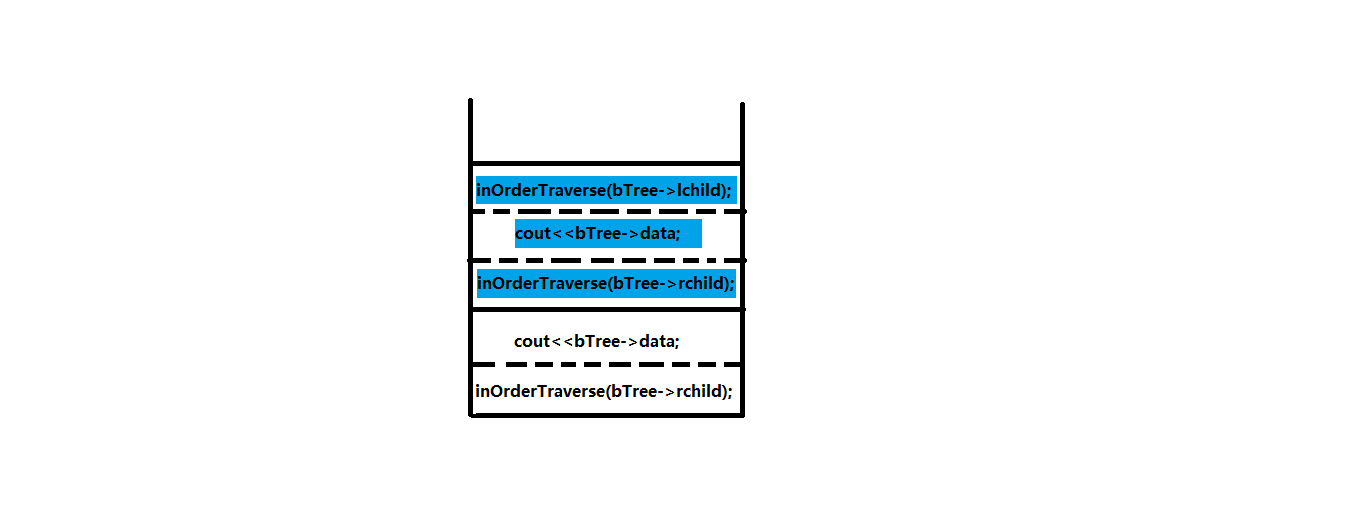
显而易见，这就是一个出栈入栈的过程。函数保存在栈帧中的操作和数据，我们可以通过自定义的栈来储存。

2.2. 非递归的实现

如果，栈中可以存放操作语句，那非递归的实现将会变得十分容易，可惜，栈中只能存放数据。

不过，幸运的是，递归的操作都是重复的，我们只要将数据统一，并根据数据进行相对应操作即可。

在树的递归遍历中，其实只有一个操作，那就是输出结点数据，而剩余函数只是个入栈的过程。

以中序递归遍历为例：

1. 依次将右孩子（第二个子函数）、根结点（输出数据操作）、左孩子（第一个子函数）入栈。

2. 然后检测栈顶过程中，遇到不为空的左/右孩子，则重复上述入栈操作；遇到根结点则输出数据；栈顶指针为空则出栈。

但是，如何判断是孩子、还是根结点呢？我认为可以有两种方法：

（1）设计一个结构体作为栈基本单位。该结构体有两个值：一个用来判断是根结点（根结点则输出数据）还是孩子（孩子则右-根-左入栈）的标志位，另一个是指向树的指针：

// 中序遍历，非递归第一种方法
typedef struct {
    bool flag;      // 用来判断是根结点(true)还是孩子(false)
    BiTree bTree;   // 树指针
}Node;

void inOrderTraverse1(BiTree bTree) {
    if (!bTree) {
        cout<<"该树为空！";
        return;
    }

    cout<<"非递归中序遍历：";
    stack<Node> s;
    Node temp, top;
    temp.flag = false;
    temp.bTree = bTree;
    s.push(temp);
    while (!s.empty()) {
        top = s.top();
        s.pop();
        // 如果栈顶树指针为空，则不操作
        if (top.bTree == NULL) continue;
        // 如果是根结点
        if (top.flag) {
            cout << top.bTree->data;
        }
        // 如果是孩子
        else {
            temp.flag = false;
            temp.bTree = top.bTree->rchild;
            s.push(temp);

            temp.flag = true;
            temp.bTree = top.bTree;
            s.push(temp);

            temp.flag = false;
            temp.bTree = top.bTree->lchild;
            s.push(temp);
        }
    }
    cout << endl;
}

（2）将树结点作为栈的基本单位。设置一种数据结点，只存放数据，而左右孩子为空。每次检测栈顶结点，若左右孩子为空则输出，否则依次将不为空的右孩子、根结点的数据结点、不为空的左孩子入栈：

// 中序非递归遍历，第二种算法
void inOrderTraverse2(BiTree bTree) {
    if (!bTree) {
        cout<<"该树为空！";
        return;
    }

    cout<<"非递归中序遍历：";
    stack<BTNode> s;
    s.push(*bTree);
    BTNode temp, dataBTNode;
    dataBTNode.lchild = dataBTNode.rchild = NULL;
    while (!s.empty()) {
        temp = s.top();
        s.pop();

        if (!temp.lchild && !temp.rchild) cout<<temp.data;
        else {
            dataBTNode.data = temp.data;

            if (temp.rchild) s.push(*temp.rchild);
            s.push(dataBTNode);
            if (temp.lchild) s.push(*temp.lchild);
        }
    }
    cout<<endl;
}

3. 后话

实际上，递归并非我们想象中那么拖慢效率。在不至于递归栈爆的情况下，我们还是可以放心地使用递归的。