吴恩达深度学习第一课笔记 - 神经网络与深度学习
0. 前言
观看吴恩达深度学习视频的学习笔记。
此为第一课——神经网络与深度学习,共四周。
最后,B站牛逼。
1. 第一周 - 深度学习概论
1.1. 欢迎
课程简介,共5课:

1.2. 什么是神经网络
略
1.3. 用神经网络进行监督学习
神经网络在监督学习中的应用:

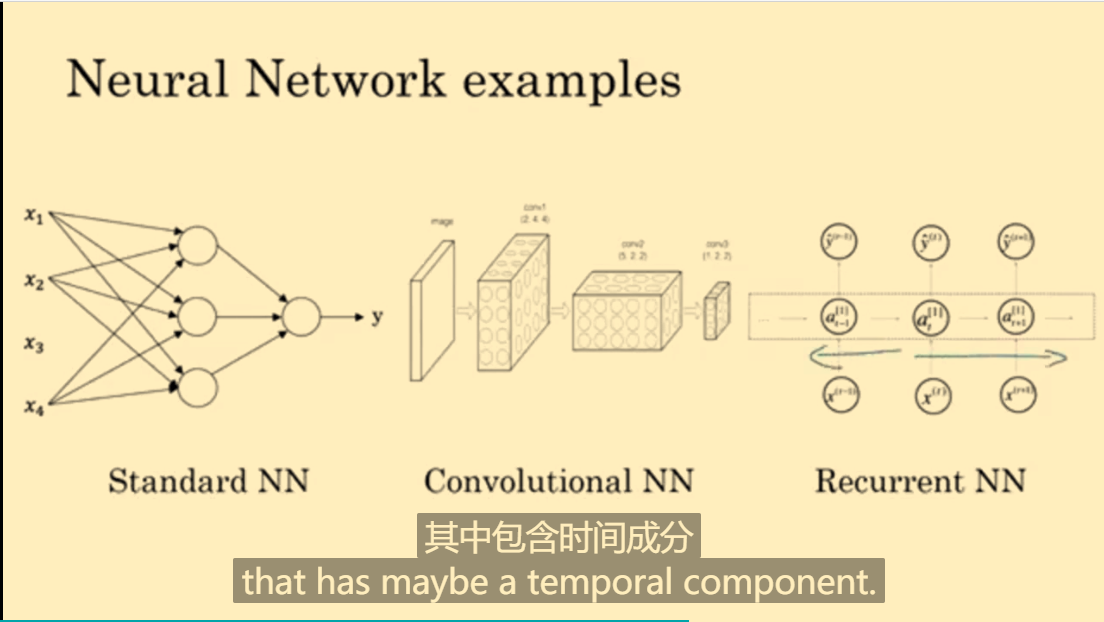
几种神经网络的图例:
Standard NN:标准神经网络Convolution NN(CNN):卷积神经网络Recurrent NN(RNN):递归神经网络
结构化数据(数据库数据)与非结构化数据(音频、图片、文字):

1.4. 为什么深度学习会兴起
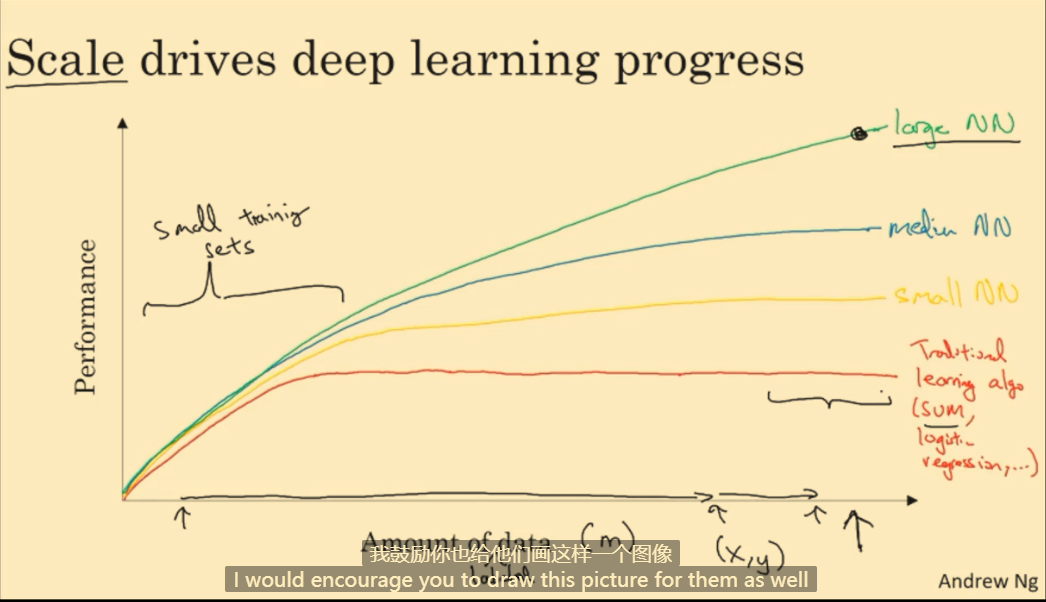
当训练集较小时,各算法难分高下;当训练集足够大时,神经网络算法的性能要优于大部分机器学习算法。
随着数据规模和计算能力的发展,深度网络兴起了。
注:训练集(x, y)是由输入x和标签y组成的,m表示训练集大小。
1.5. 关于这门课
略
1.6. 课程资源
略
2. 第二周 - 神经网络基础
2.1. 二分分类
二分类:标签值 $y$ 要么为 0 要么为 1
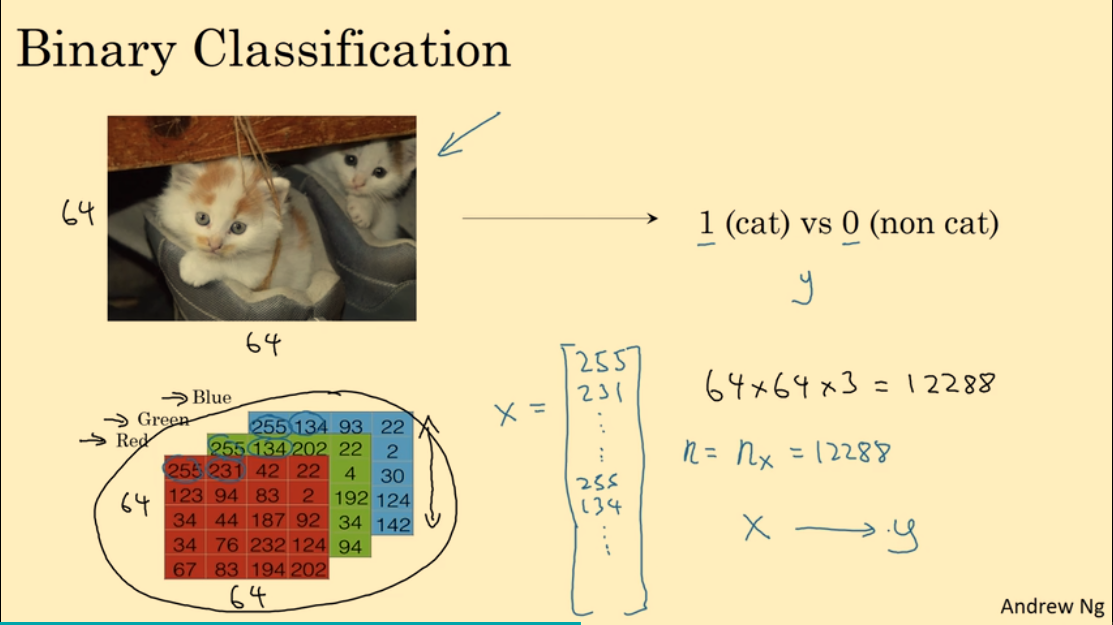
一些符号的定义:
- $n$ 或 $n_x$:表示输入特征向量的维度
- $x \in R^{n_x}$:输入的特征向量
- $y \in {0, 1}$:标签值为0或1
- $(x, y)$:一个训练样本
- $m$:训练集的大小
- $(x^{(i)}, y^{(i)})$:表示训练集中第i个训练样本
- $X$:整个训练集的输入特征向量构成的矩阵,矩阵的维度为$(n_x, m)$
- $Y$:整个训练集的输出标签构成的矩阵,矩阵的维度为$(1, m)$

2.2. logistic 回归
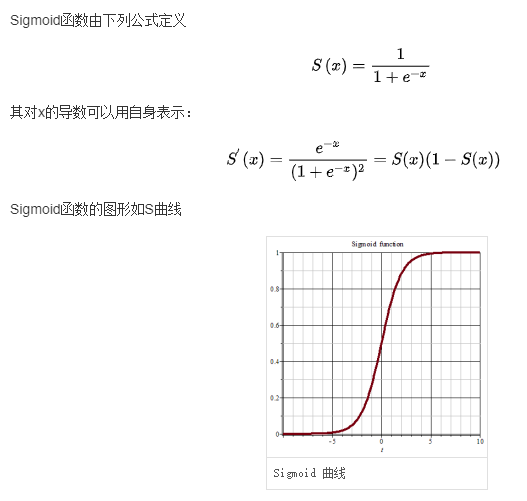
用 logistic 回归(逻辑回归)解决二分类问题:$\hat{y} = sigmoid(w^Tx+b)$。注意:此处使用 $w^Tx+b$,而不使用 $\theta^Tx$。

sigmoid 函数(是一种 logistics 函数)相关定义如下:
2.3. logistic 回归损失函数
由上可知:$\hat{y}^{(i)} = sigmoid(w^Tx+b)$:第i个样本的预测值。
损失函数(Loss function) 使用:
$L(\hat{y}, y) = -[y log\hat{y} + (1-y) log(1-\hat{y})]$
注意:此处不使用平方差:$L(\hat{y}, y) = \frac{1}{2}(\hat{y}-y)^2$,因为这是个二次函数,容易得到多个局部最优解,使用梯度下降法可能找不到全局最优值。
损失函数在单个训练样本中定义,它衡量了参数 w 和 b 在单个训练样本上的表现。
成本函数(cost function) 则衡量参数 w 和 b 在全体训练样本上的表现,如下:
$J(w,b) = \frac{1}{m} \displaystyle \sum_{i=0}^nL(\hat{y}^{(i)}, y^{(i)})$
在训练 logistics 回归模型时,我们就是要找到合适的 w 和 b,让成本函数尽可能地小。

2.4. 梯度下降法
我们训练模型的目的是:找到合适的 w 和 b 使得 $J(w, b)$ 最小。
假设 w 和 b 是一维变量,$J(w, b)$ 的图像如图,它是一个凸函数,只有一个全局最小值。而我们的目的,就是找到这个最小值。
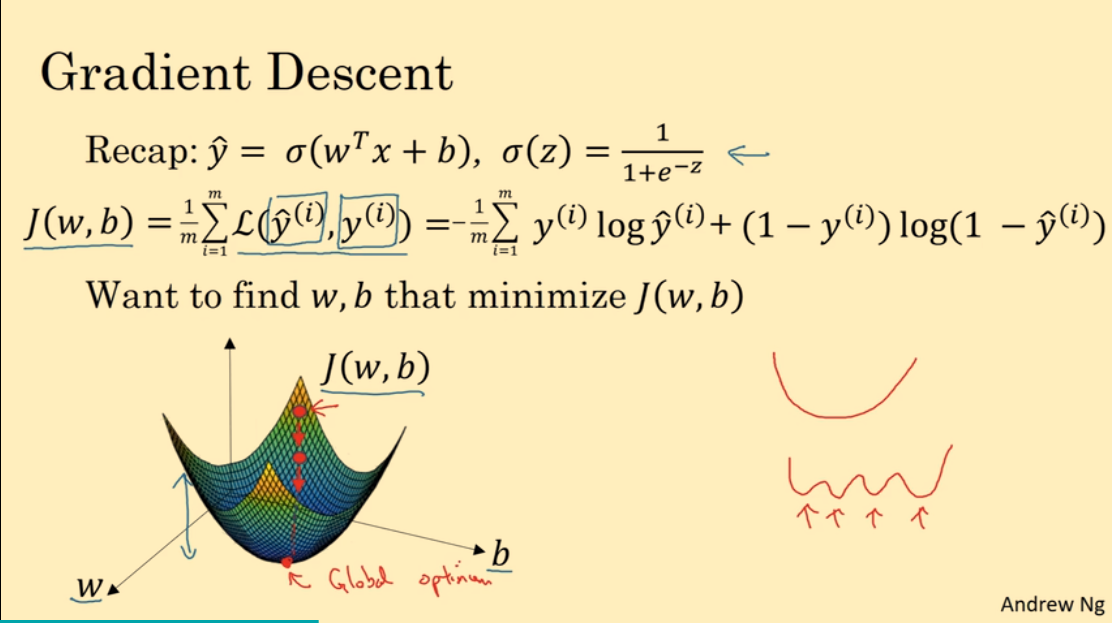
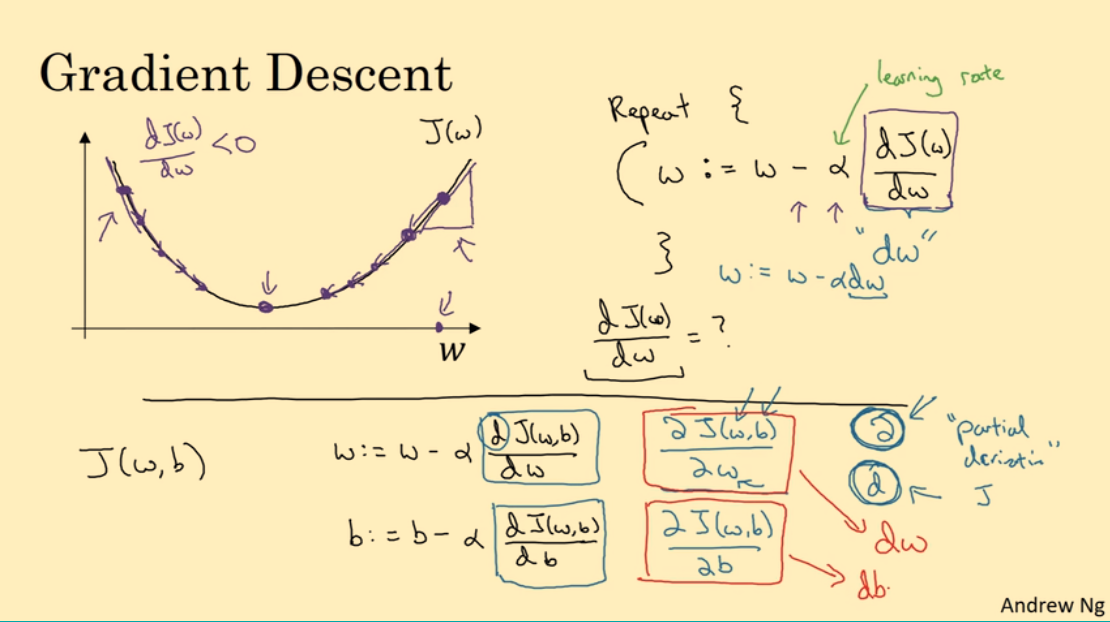
假设 $J(w)$ 是一个一维函数,且是一个凸函数。
我们可以通过梯度下降法找到最小值。$w$ 初始位置任意,为了找到 $w$ 使得 $J(w)$ 最小,我们只需要重复如下步骤:
$w := w-\alpha \frac{dJ(w)}{dw}$
- $\alpha$:学习率,表示每一步 $w$ 变化的步长,决定 $J(w)$ 下降的速度。
- $\frac{dJ(w)}{dw}$:导数,$(w, J(w))$ 处的斜率。
在曲线越陡峭的地方,导数越大,$w$ 变化得越大,$J(w)$ 下降得越快;在曲线较缓和的地方,导数较小,$w$ 变化得小,$J(w)$ 下降得也慢。
2.5. 导数
略
2.6. 更多导数的例子
略
2.7. 计算图
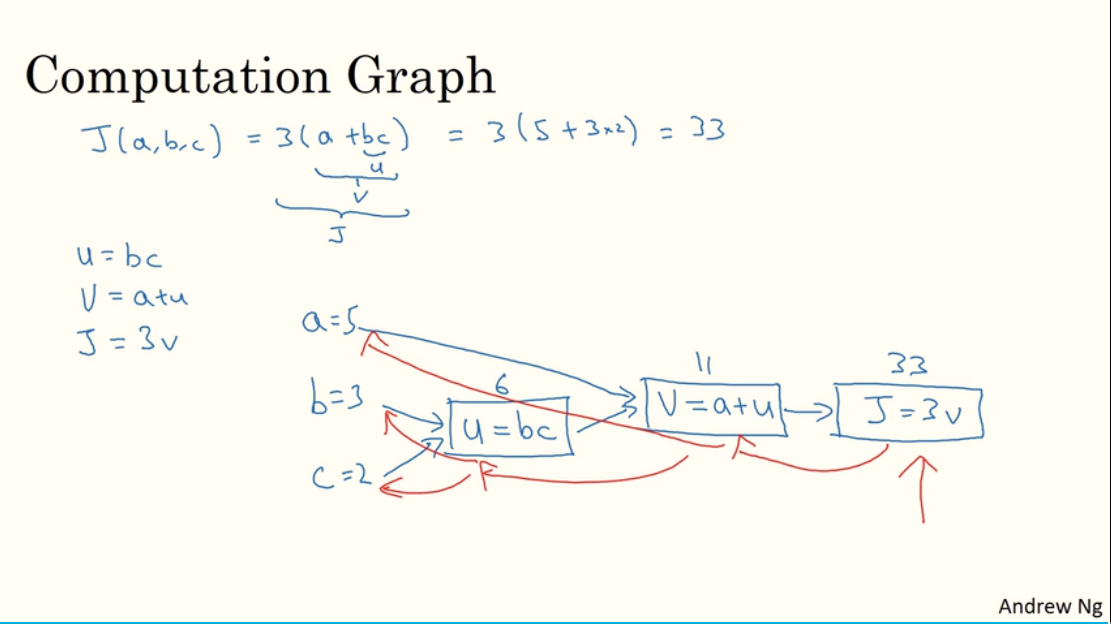
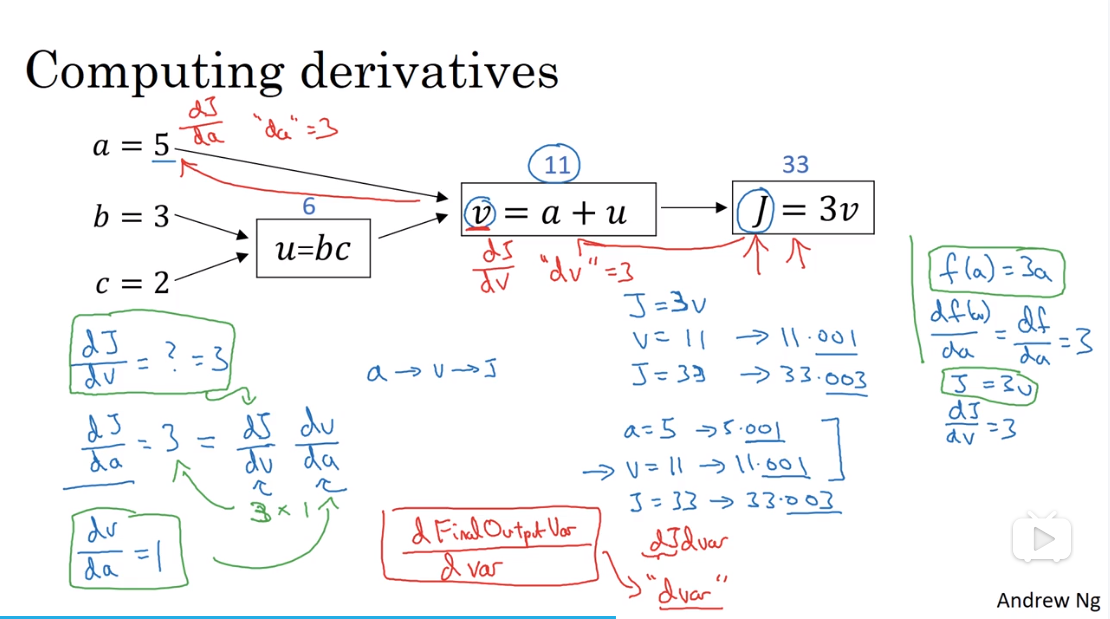
2.8. 计算图的导数计算
注:$\frac{dFinalOutputVar}{dvar}$ 可看成 $dvar$

2.9. logistics 回归中的梯度下降法
注:$L(a, y) = -[y loga + (1-y) log(1-a)]$

2.10. m 个样本的梯度下降
注:$J = \frac{1}{m} \displaystyle \sum_{i=0}^nL(\hat{y}^{(i)}, y^{(i)})$
在计算完 m 个样本上的累计误差/成本函数 $J$ 和得到参数的累计梯度 $dw_i$ 之后,再进行参数更新。

在之后的课程中,将提到用向量化Vectorization改善for循环。
2.11. 向量化
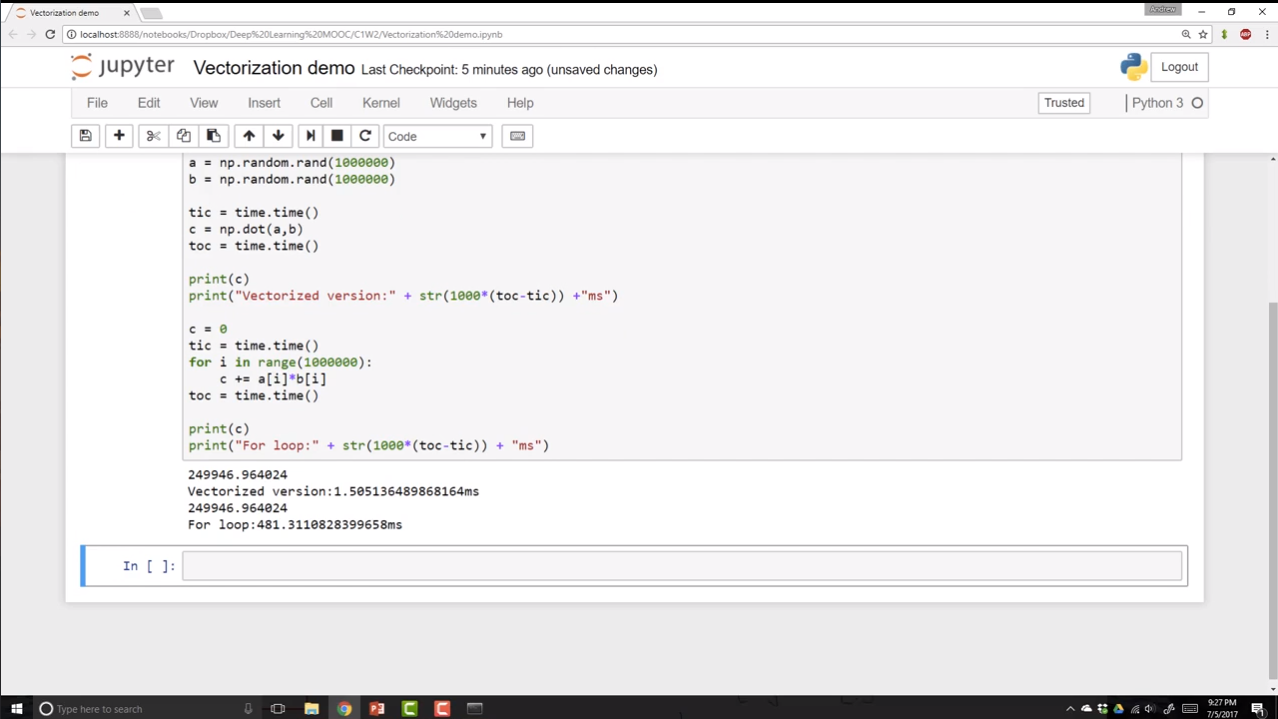
向量化:用 np.dot() 代替 for 循环。(其实,这是因为 numpy 底层用 C 实现,所以比 python 的 for 循环快很多,归根到底还是循环实现)
2.12. 向量化的更多例子

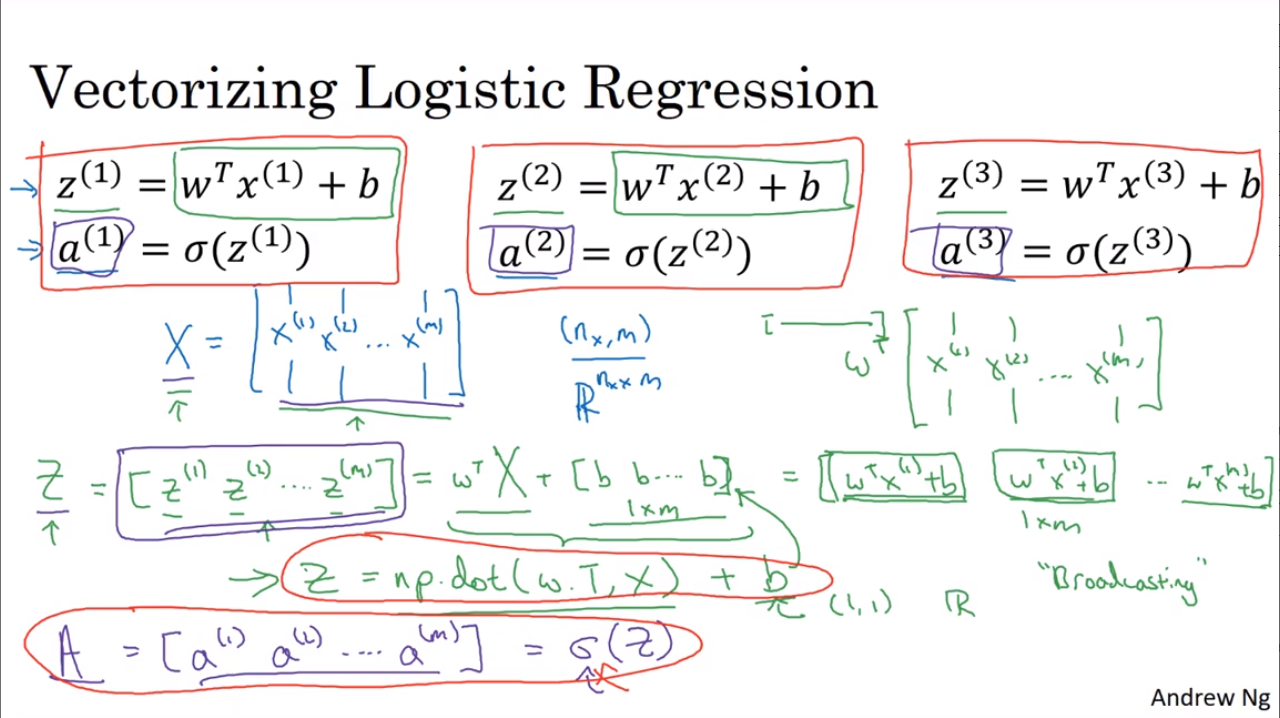
2.13. 向量化 logistic 回归
2.14. 向量化 logistic 回归中的梯度输出
下图左边是未使用向量化的代码,右边是使用了向量化的代码(其实就是 numpy 库)。

2.15. python 中的广播
numpy 的广播。
2.16. 关于 python_numpy 向量的说明
略
2.17. Jupyter Ipython 笔记本的快速指南
略
2.18. logistic 损失函数的解释
在 logistic 回归中,可以把预测值 $\hat{y}$ 看作在 $x$ 条件下 $y$ 取 1 的概率;而 $1-\hat{y}$ 可以看作在 $x$ 条件下 $y$ 取 0 的概率。
注:在二分类问题中,$y$ 只有 1 或 0 两种取值。
综合两种情况,在 $x$ 条件下 $y$ 取 0 或 1 的概率为 $p(y|x) = \hat{y}^y (1-\hat{y})^{(1-y)}$ (下图中有解释)。
如果想让 $p(y|x)$ 最大,可以先让 $log p(y|x)$ 最大(log 是单调函数)。
而 $log p(y|x) = ylog\hat{y} + (1-y)log(1-\hat{y})$ 。
同时,结合上文提到的损失函数,我们可以发现: $log p(y|x) = -L(\hat{y}, y)$ ,当损失函数最小时,$y$ 取期望值的概率就越大。

如果想获得 m 个样本都取到期望值的概率 $P$,那应该将每个样本的概率相乘,即:$P = \displaystyle\prod_{i=1}^m p(y^{(i)}|x^{(i)})$。
如果使用最大似然估计,那需要找到一组参数使得 $P$ 的值最大。而令 $P$ 值最大,等价于令 $logP$ 最大。
由于 $logP = \displaystyle\sum_{i=1}^m log p(y^{(i)}|x^{(i)})$ ,进而可得:$logP = -\displaystyle\sum_{i=1}^mL(\hat{y}, y)$。
最后,当成本函数 $J(w,b) = \frac{1}{m} \displaystyle\sum_{i=0}^nL(\hat{y}^{(i)}, y^{(i)})$ 取最小值时,$logP$ 取最大值,也就是 $P$ 取最大值(m 个样本都取到期望值的概率最大)。

3. 第三周 - 浅层神经网络
3.1. 神经网络概览
约定:用 $W^{[i]}$ 上标表示第 $i$ 层的参数。