吴恩达深度学习第四课笔记 - 卷积神经网络
0. 前言
软件杯需要,先略看第四课。
1. 卷积神经网络
1.1.计算机视觉
计算机视觉中一些待解决的问题:
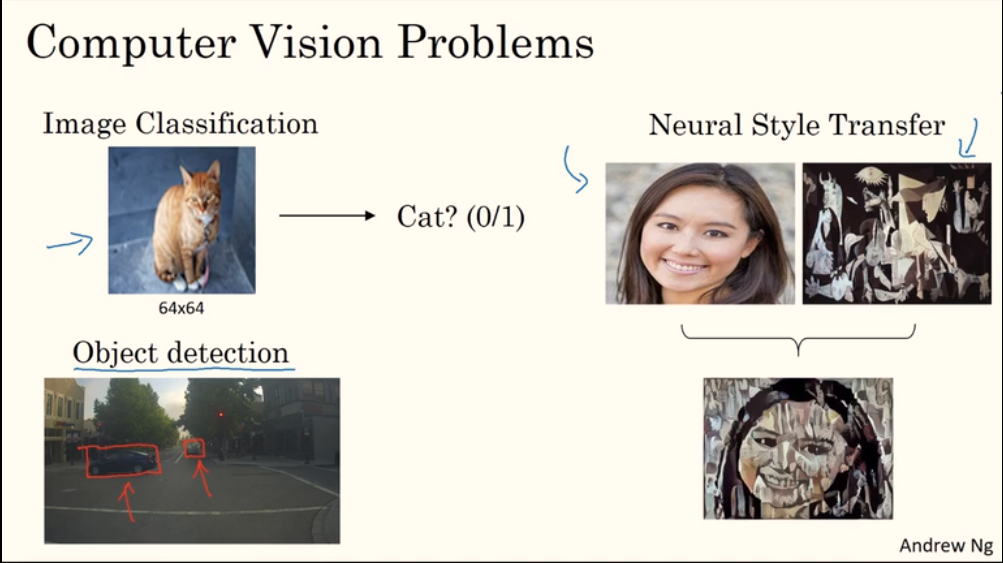
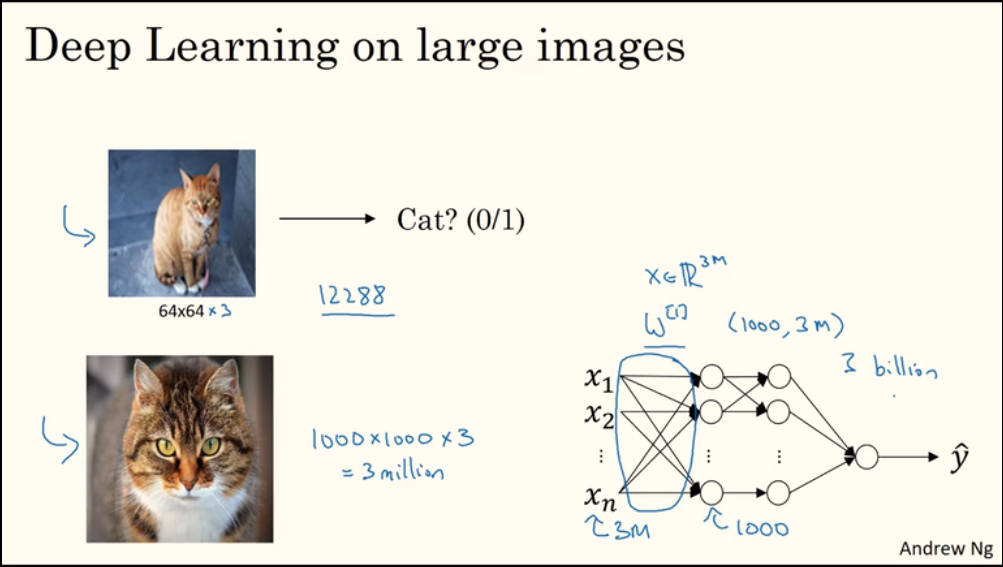
1.2. 边缘检测示例
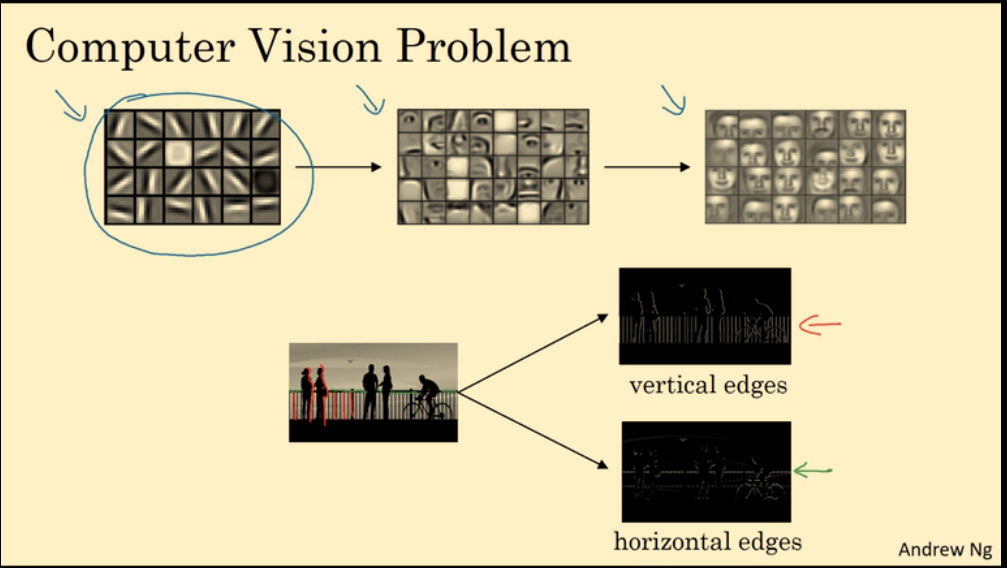
识别图片中的物体,第一步通常是检测图片中的垂直边缘、水平边缘。(边缘:edge,应该是指在图片中明显的分割线)
用卷积运算检测出垂直边缘。filter 被称作:滤波器,或者卷积核:
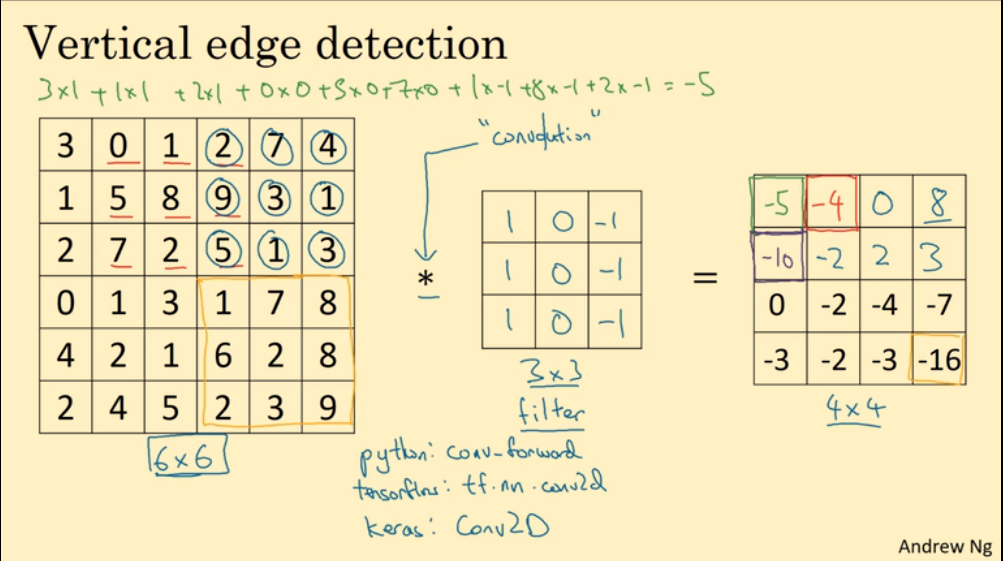
为什么这个卷积运算可以检测出垂直边缘?(数值越大越亮,越小越暗。)
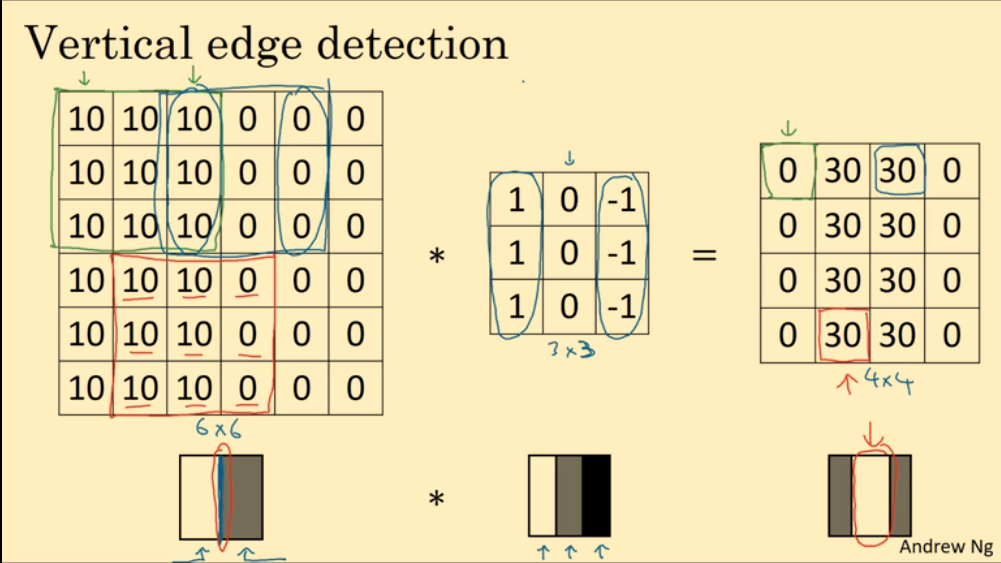
1.3. 更多边缘检测的例子
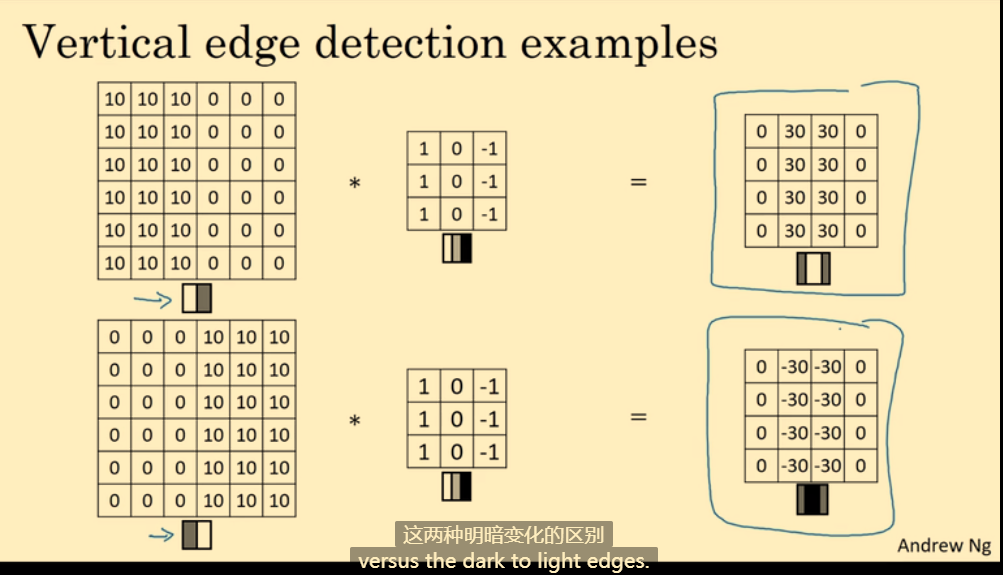
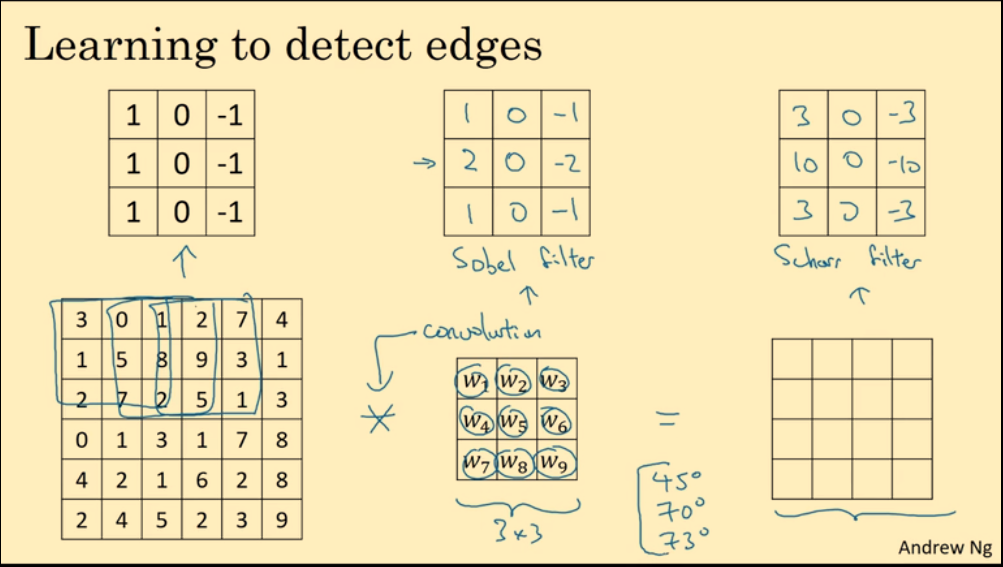
不同的滤波器,可以检测不同的边缘。Vertical 滤波器可以检测垂直边缘,Horizontal 滤波器可以检测水平边缘。
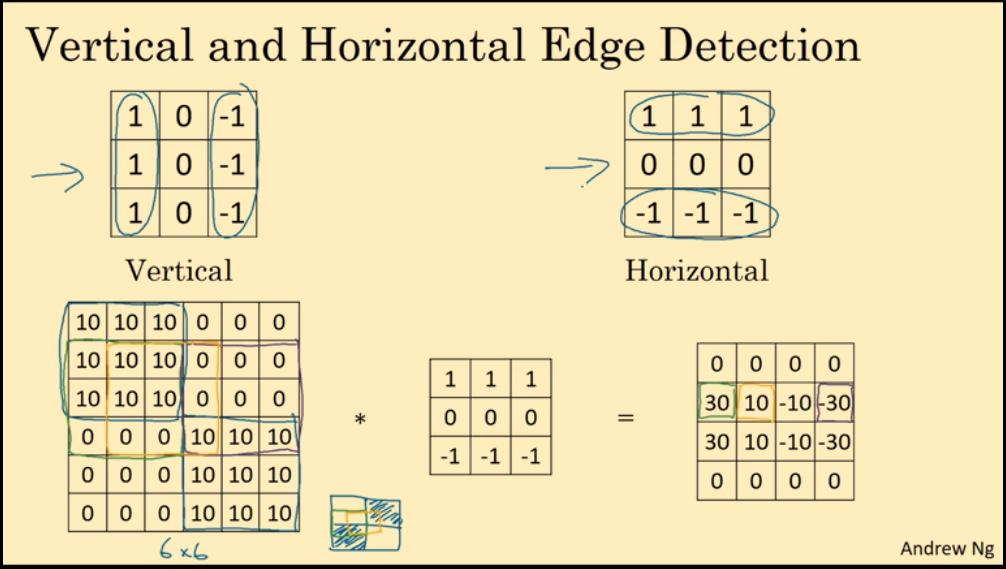
计算机视觉领域有许多经典滤波器filter,但在CNN中,滤波器的值被当作参数,经过反向传播算法进行学习,最终得到更加有用的滤波器filter。
1.4. padding
padding:在图片四周添加填充像素点(填充值一般是0):
- 防止多次卷积后图像太小
- 防止边界信息丢失
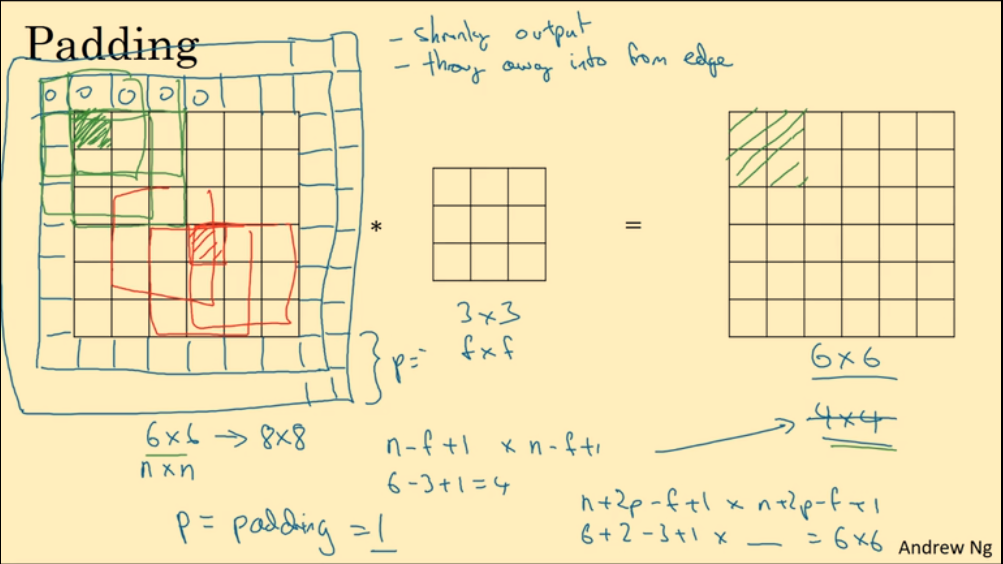
Valid卷积运算,对原图像不添加padding:$n \times n * f \times f \longrightarrow (n-f+1) \times (n-f+1)$Same卷积运算,对原图像添加padding使得输出图像大小与输入图像大小相等:$(n+2p) \times (n+2p) * f \times f \longrightarrow (n+2p-f+1) \times (n+2p-f+1) = n \times n$

1.5. 卷积步长
步长:每次运算后移动的格数。如下图,步长为2,运算完第一次后,向右移动2格。
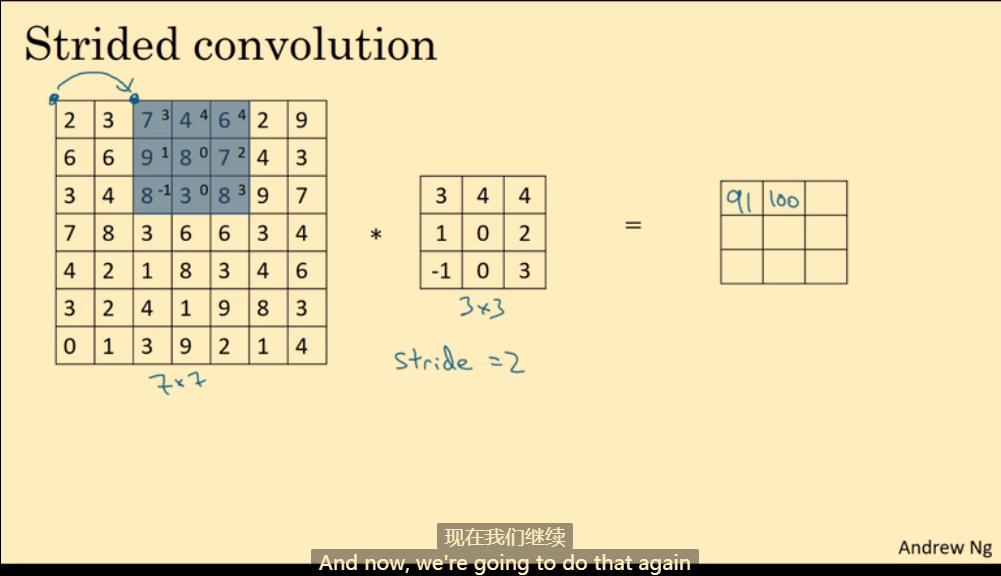
同理,运算完第一行后,向下移动两格。
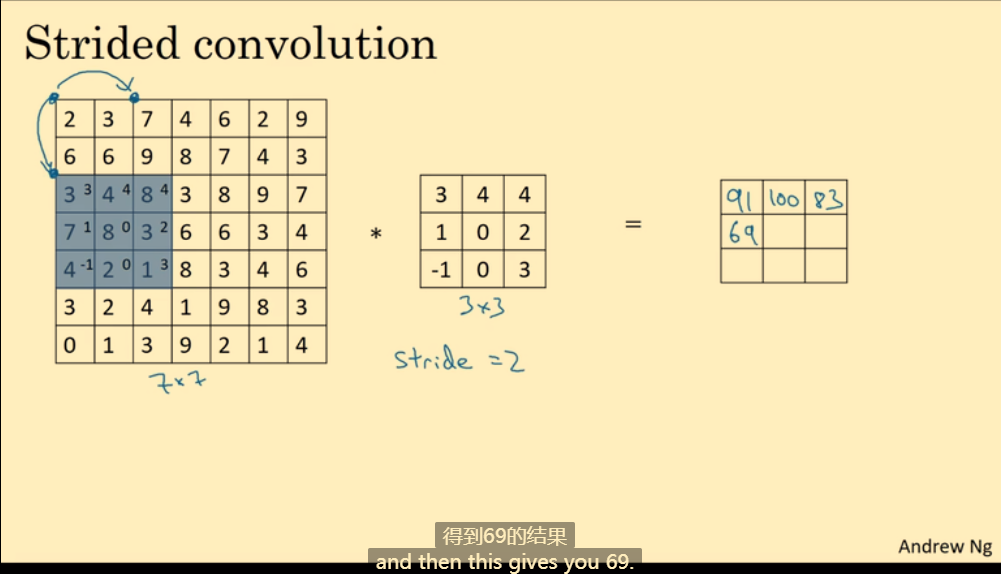
结合padding和步长后,输出图像的大小计算公式(结果向下取整):

在某些数学文献中,卷积运算又被称为互相关(cross-correlation),在运算之前需要对filter进行翻转。但在深度学习领域,一般叫做卷积运算,也不进行filter翻转。

1.6. 三维卷积
对于一张RGB图像,它的像素值通常是三维立体。例如一张6x6的RGB图像,它实际是6x6x3,第一个6代表高,第二个6代表宽,3代表通道数channel(即R、G、B三值)。
三维卷积运算中,filter滤波器也是三维的,并且filter的通道数必须与图像的通道数相等。值得注意的是,最后输出的图像是二维的。
在下图的例子中,输入图像的第一个3x3x3立方体与filter进行运算:配对位置相乘,最后将27个相乘结果相加,填入4x4输出图像的第一个位置中。

多个filter滤波器:不同滤波器检测不同的图像特征,最后输出图像是三维的,它的通道数等于滤波器的个数。
下图的例子中,使用了两个filter滤波器,一个检测垂直边缘,一个检测水平边缘,最后得到2个4x4图像,即结合成4x4x2的图像。
1.7. 单层卷积网络
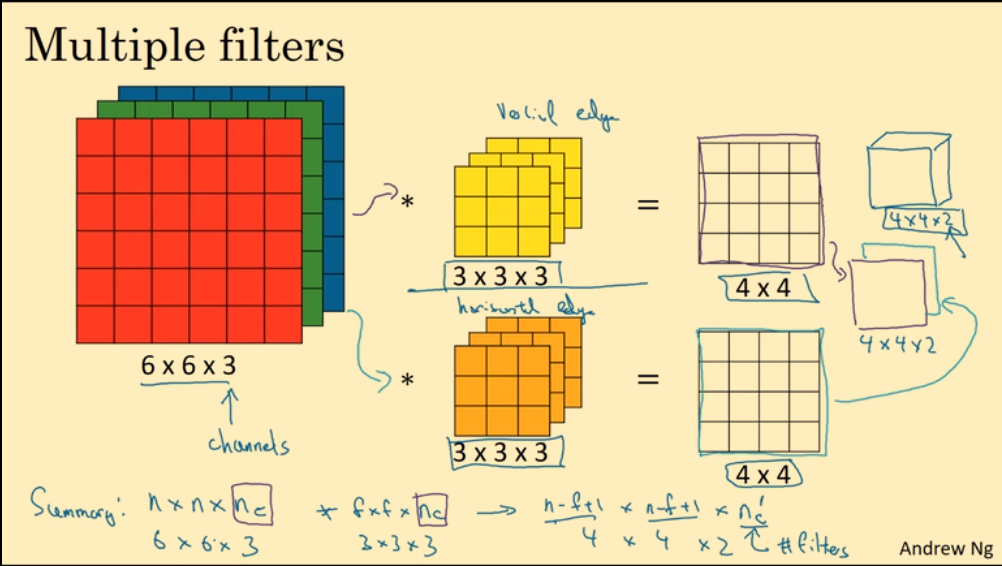
在下图的单层卷积网络示例中,6x6x3 输入图像作为输入 $a^{[0]}$,多个滤波器filter作为权重 $w^{[1]}$,不同filter的卷积运算结果加上对应差值 $b_i$,再通过激活函数,最终得到输出 $a^{[1]}$(4x4x2 输出图像)。
$$
a^{[1]} = g(w^{[1]} a^{[0]} + b^{[1]})
$$
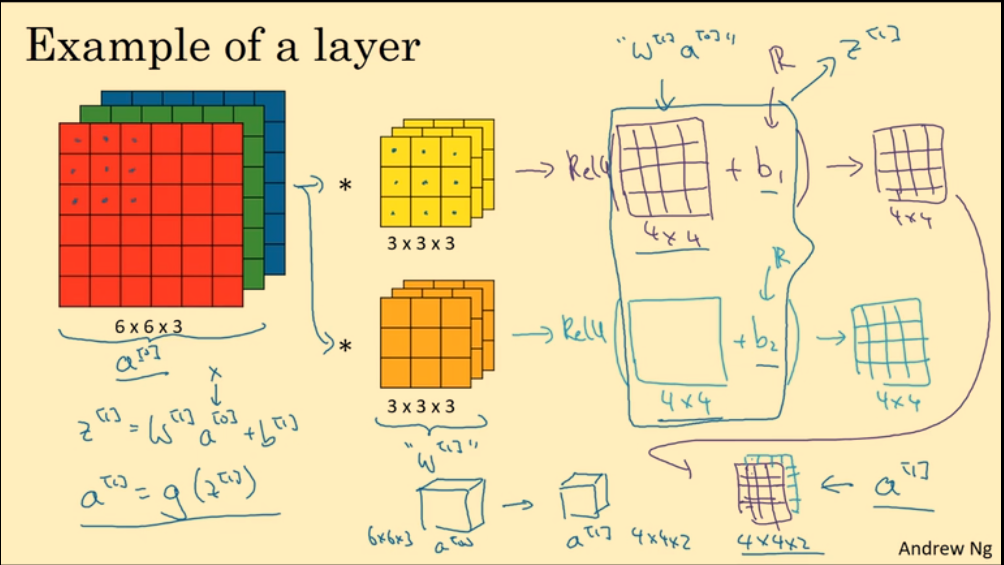
计算单层卷积网络的参数:假如一层有10个 3x3x3 的filter,那一个filter将有27个参数,外加一个差值b参数,总共28个参数,10个filter即有280个参数。

一些符号的约定:

1.8. 简单卷积网络示例

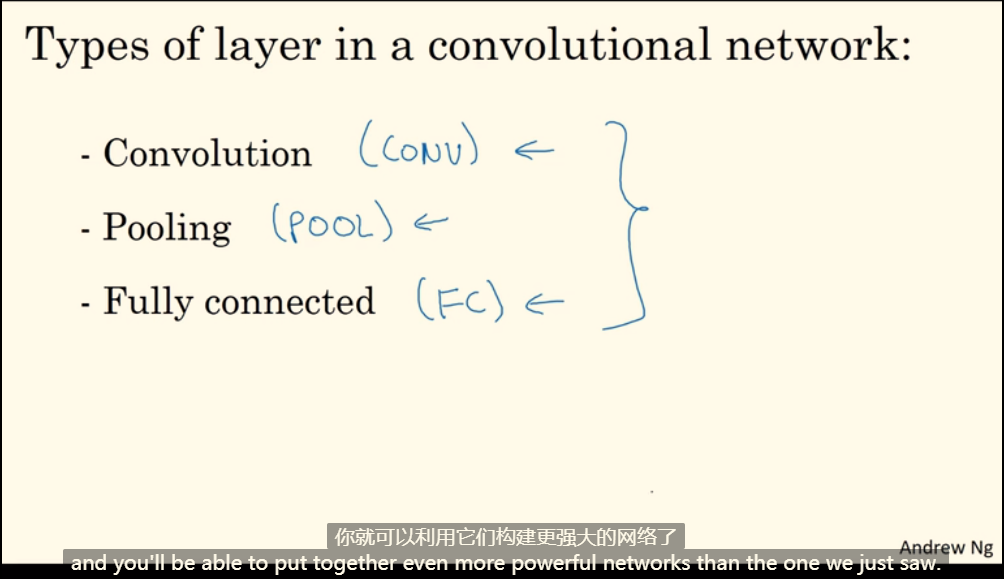
卷积网络中不同类型的层:
- 卷积层(Convolution,CONV)
- 池化层(Pooling,POOL)
- 全连接层(Fully connected,FC)
1.9. 池化层
池化:对一个 nxn 区域提取特征值。
池化的作用:我认为是提取主要特征、信息过滤,是向计算性能妥协的过程。
如下图,使用了最大池化的方法,对于输入的 4x4 图像,提取每个不重合 2x2 区域的最大值放入输出图像中。
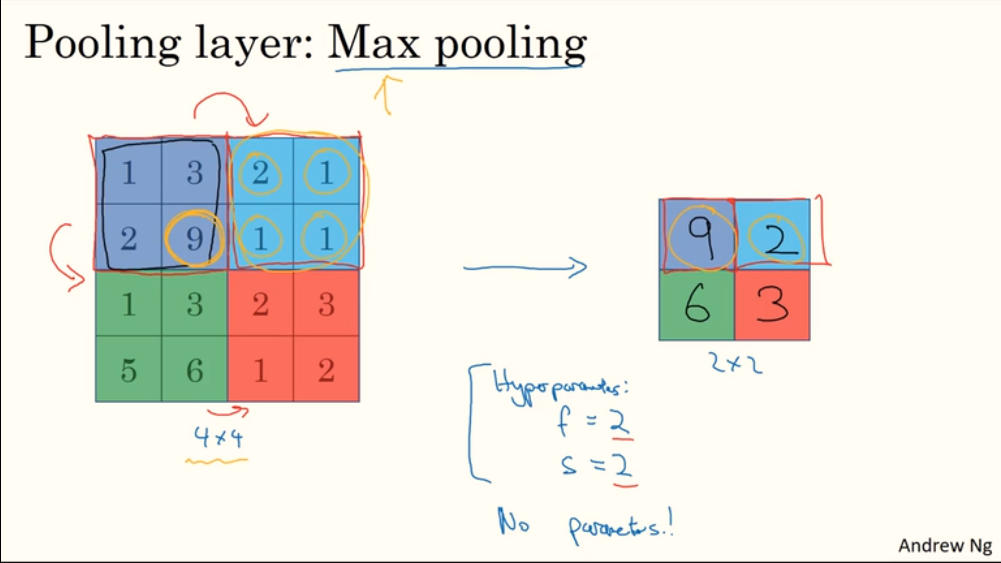
在池化计算中,输出图像信道数一定与输入图像信道数相同。
池化也可以设置filter大小和步长参数,如下图 $f=3$、$s=1$(应用较多的是 $f=2$、$s=2$)。值得注意的是,这些参数没有学习的必要,它们是静态参数。
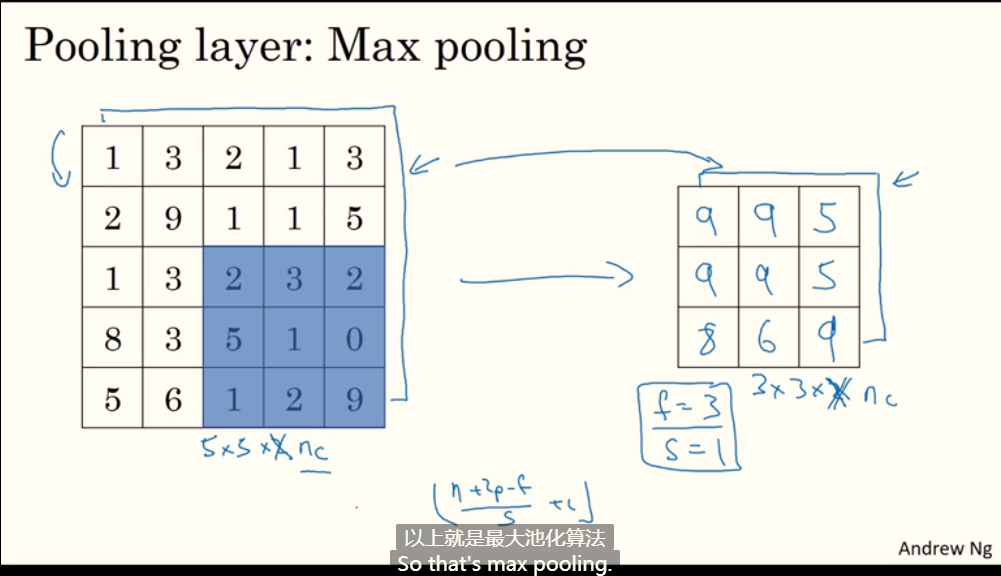
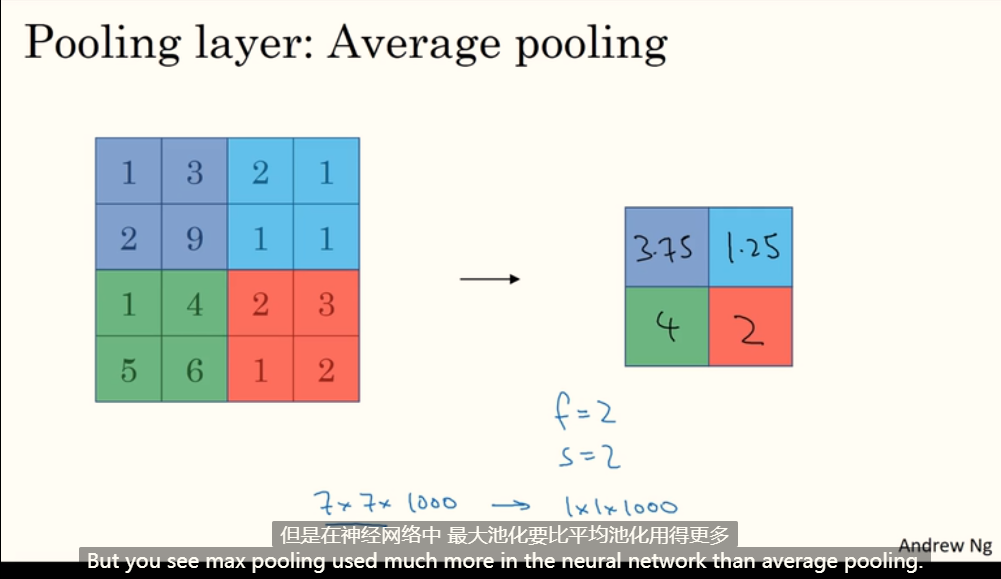
平均池化:
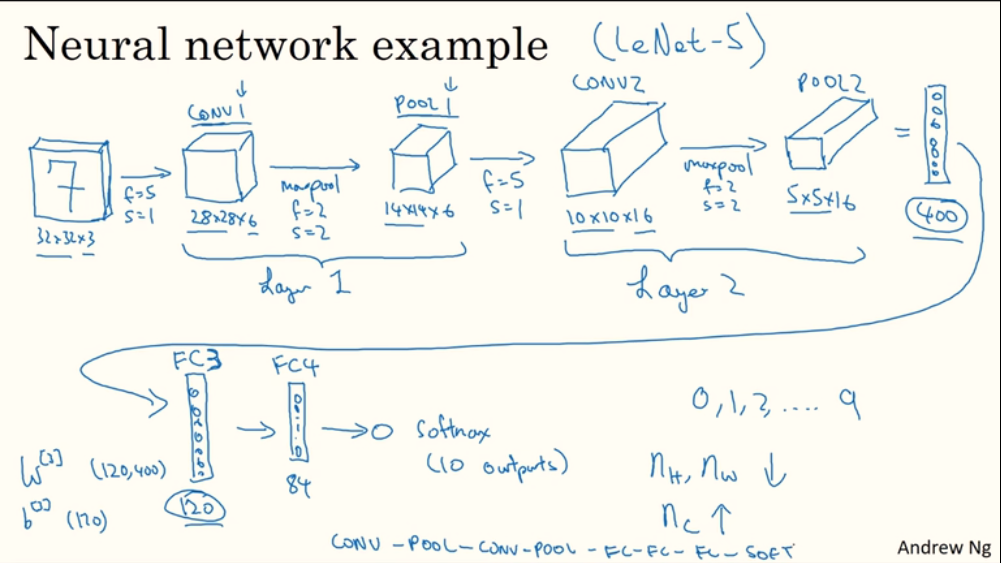
1.10. 卷积神经网络示例
输入一张 32x32x3 的图像。
第一层卷积层:经过一次卷积(6个
filter)、一次最大池化,得到 14x14x6 的图像(此处将一次卷积和一次池化看成一层卷积层,也有把它们分开看作两层的)。第二层卷积层:经过卷积(16个
filter)、池化,得到 5x5x16 的图像。将 5x5x16 的图像转换成一维向量,有400个值,将其作为第三层全连接层的输入。
第三层全连接层:有120个神经元。
第四层全连接层:有84个神经元。
输出层:10个神经元。
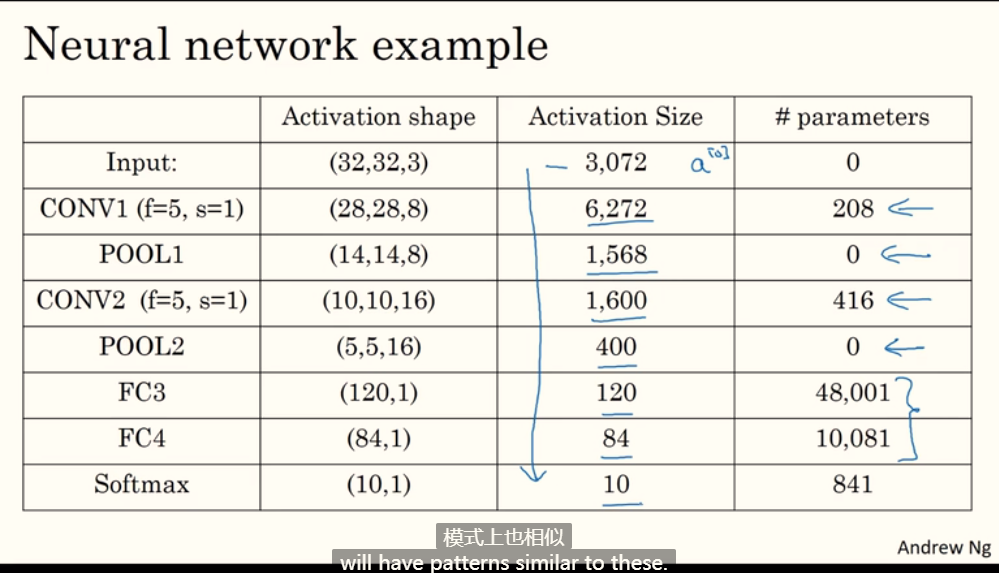
如下参数数量计算可能存在错误。
1.11. 为什么使用卷积
卷积网络参数数量远小于全连接网络:

卷积网络参数少、效率高的原因:
- 权值共享(参数共享):滤波器
filter中的一个参数(权值)被输入图像中的多个像素点共享。 - 稀疏连接:输出图像中的一个像素点仅与输入图像中部分像素点关联。
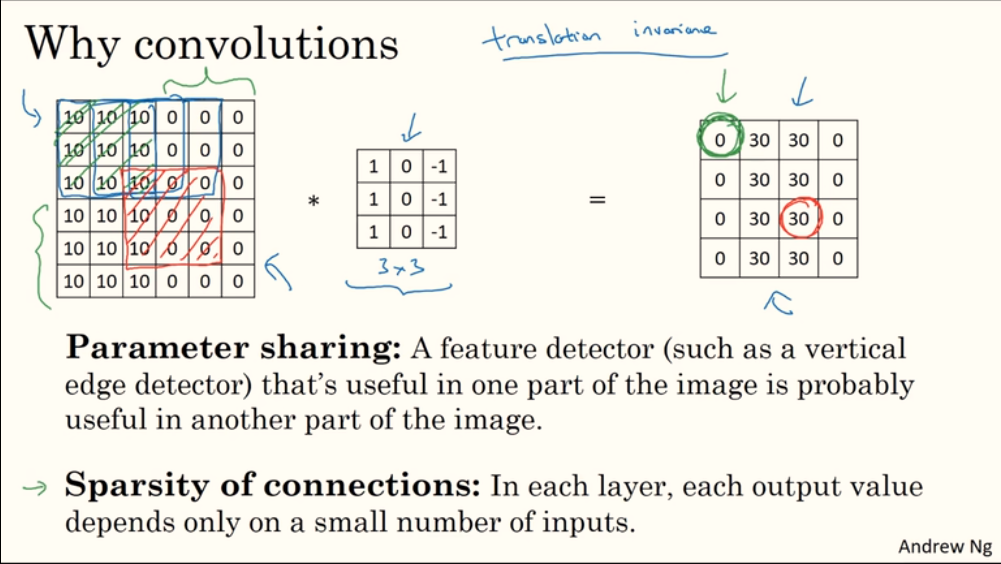
一个猫检测器示例:
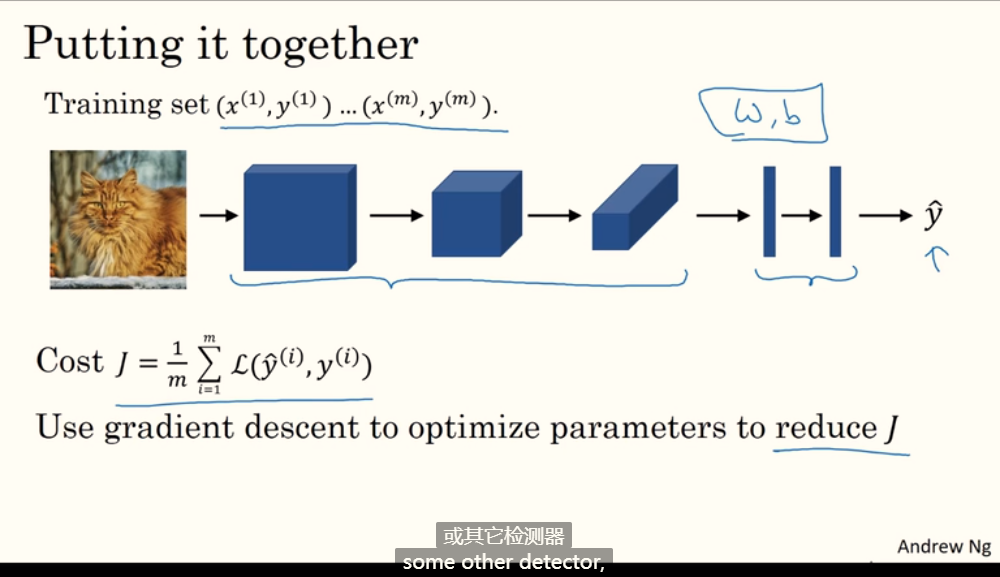
2. 深度卷积网络:实例探究
2.1. 为什么要进行实例探究
第二周大纲:

2.2. 经典网络
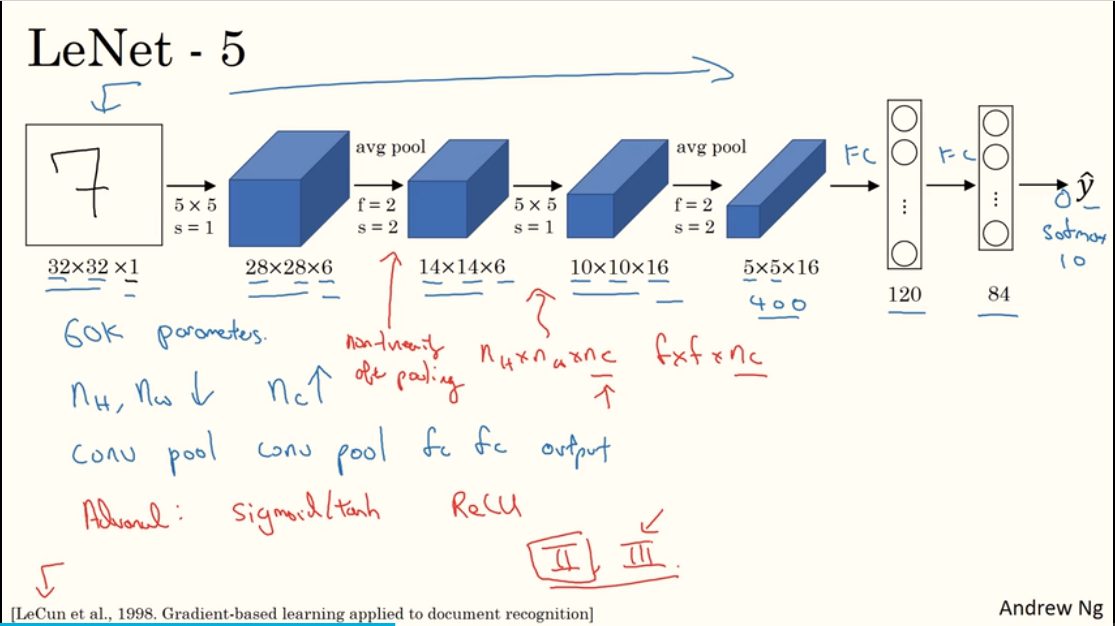
LeNet - 5:对手写数字的灰度图(32x32x1)进行分类,基本结构是:conv - pool - conv - pool - fc - fc - output,激活函数是sigmoid和tanh(论文信息见左下角)。
AlexNet:对 227x227x3 的图像进行 1000 种分类,大致的网络结构如下图。它优于LeNet的地方在于:网络更大,参数更多。
使用
ReLu激活函数。使用
Maxpooling,而不是平均pooling。使用
Dropout防止过拟合,原理很简单:根据设定的概率,选择性地丢弃当前神经元的输出,如下图: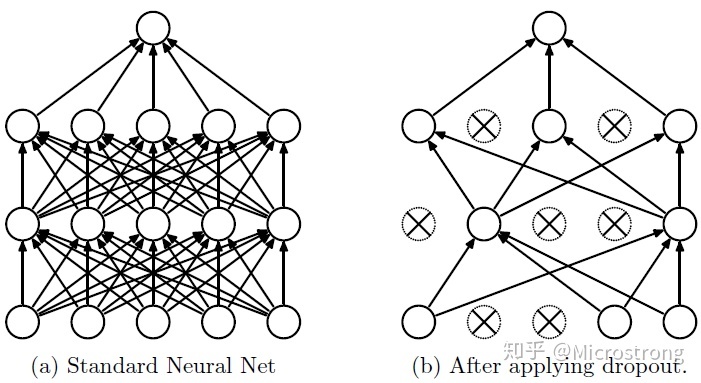
多个GPU并行计算(过时)。
使用局部响应归一层 LRN (没啥用?已过时)。
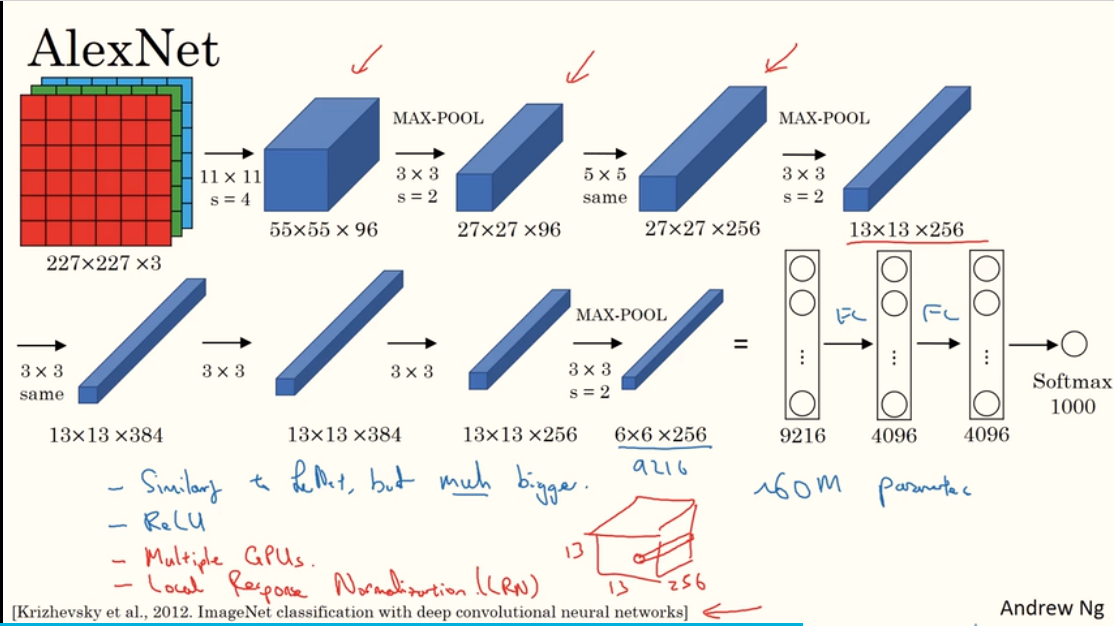
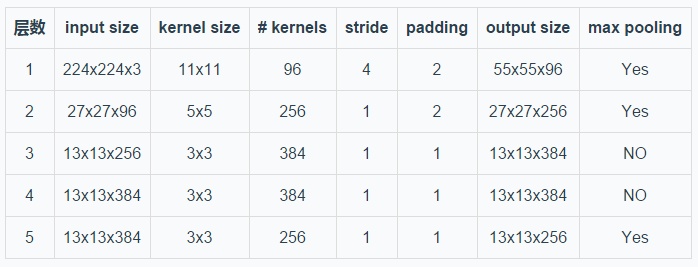
AlexNet 的5层卷积层如下(224x224加2padding结果 约等于 227x227加0padding结果,论文的描述问题,不关键):
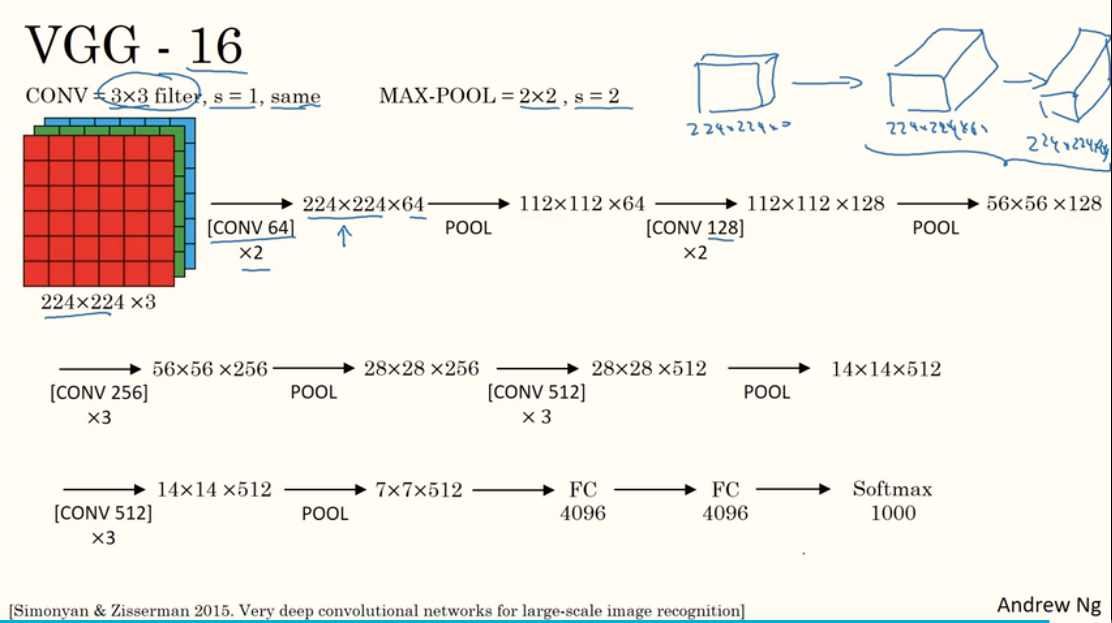
VGG - 16:16代表有16层网络,其主要改进之处在于多个卷积层后再接一个池化层,基本结构如下图,[CONV 64] x2表示经过两个有64个filter的卷积层,卷积的规则如图上方所示。